みなさまこんにちは、いかがお過ごしでしょうか。企画担当 Kです。年末年始、電車に乗って遠方へお出掛された方も多かったのではないでしょうか。さて、当館には質問を持って来館してくださる方が多くいらっしゃるのですが、今回はそのうち『鉄道』に関する質問のお話です。
今から数年前のこと。質問は、『鉄道のカントを求める公式に出てくる「0.127」という数字がどこから来るのか』というものでした。
1.『カント』とは何なのか?
はじめに、電車がカーブを曲がるときの話をしましょう。線路にある2本のレールの高さは異なっていて、カーブ内側のレールは低く、外側は高くなっています。この差があることによって電車は横転することなく走行できます。このレールの高低差のことを『カント』と言います。
※この実験は当館生活の科学3階『乗り物の科学』で体験できます。お越しの際はぜひお試しください。


カントを求める公式は次のとおり。

c :カント[mm]、R :曲線半径[mm]、V :カーブ通過時の速度[km/h]、G :軌間(線路幅)[mm]
2.スタッフ内での考察
実は当時、質問された方が帰られるまでにはお答えすることができませんでした。ただ、私を含めた館スタッフ数名で、閉館後に考察をし続けました。
・時速などが出てくる公式だから、重力加速度が関係しているのでは?
・カーブだから遠心力の公式が関係している?
・鉄道技術はイギリスからきているから、もしかしたら「インチ」が関連しているのでは?
日本では長さの単位として「ミリメートル」を用いていますが、海外では「インチ」が使われています。1インチは25.4ミリメートル。1インチを半分にすると、12.7ミリメートル…もしかしてこれは何か関係があるかもしれない、ということで「イギリスで作られた公式だから、ミリメートル換算によって、このような中途半端な数字が出てきたのでは?」などと考察してみたものの…とにかく資料を探しているうち、1958年に発行された『鉄道辞典』にカントを求める公式についての記述を発見しました。
3.ポイントは単位換算
傾いている電車の底面と、地面との角度をθとし、重力加速度g、カーブ走行時に発生する遠心力をαとします。(図1)
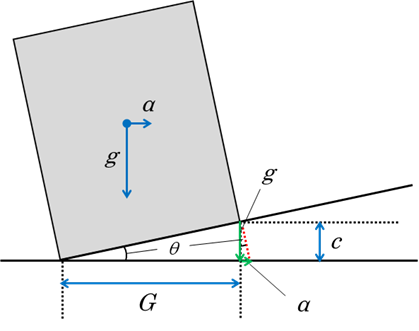
ここで中学数学に登場するtanθを考えてみましょう。まずは軌間Gと、カントcの長さの式がつくれます。
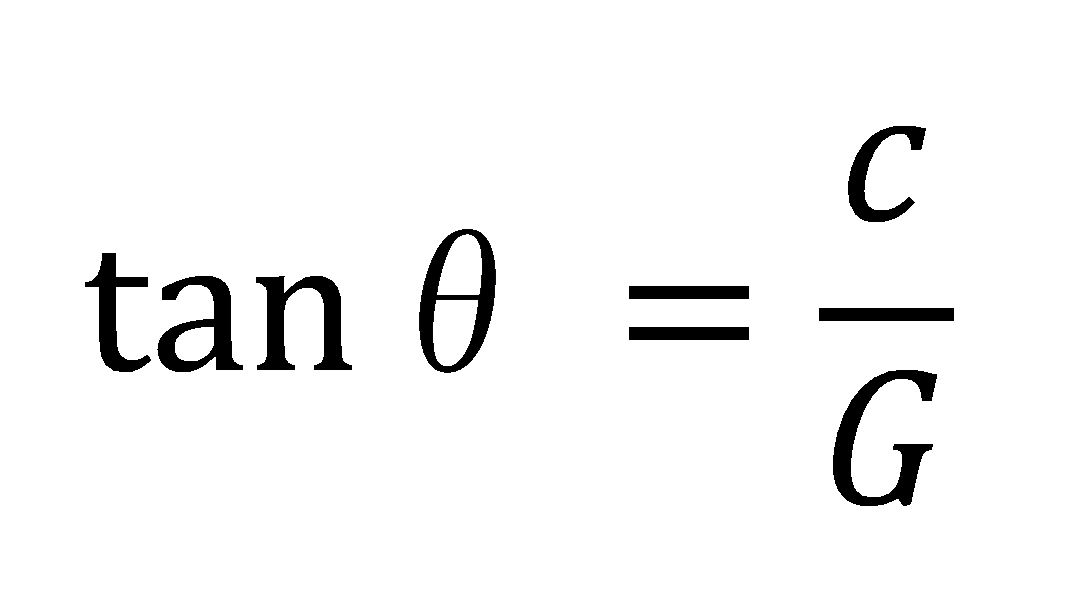
そして力の比としての式がつくれます。
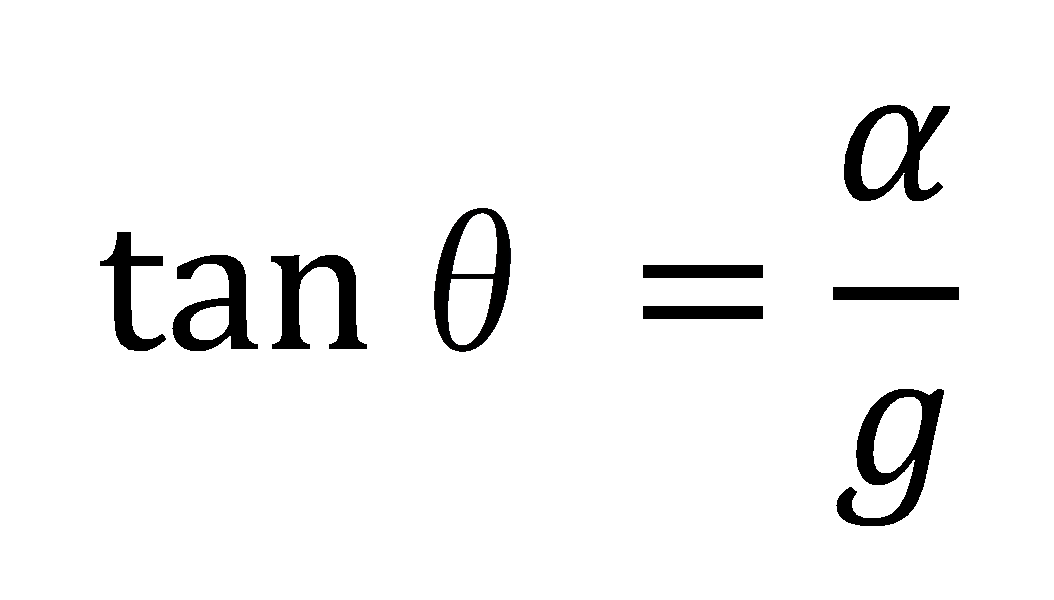
同時にカーブを通過する際に生じる遠心力の式が出てきます(これは高校物理で学習)。
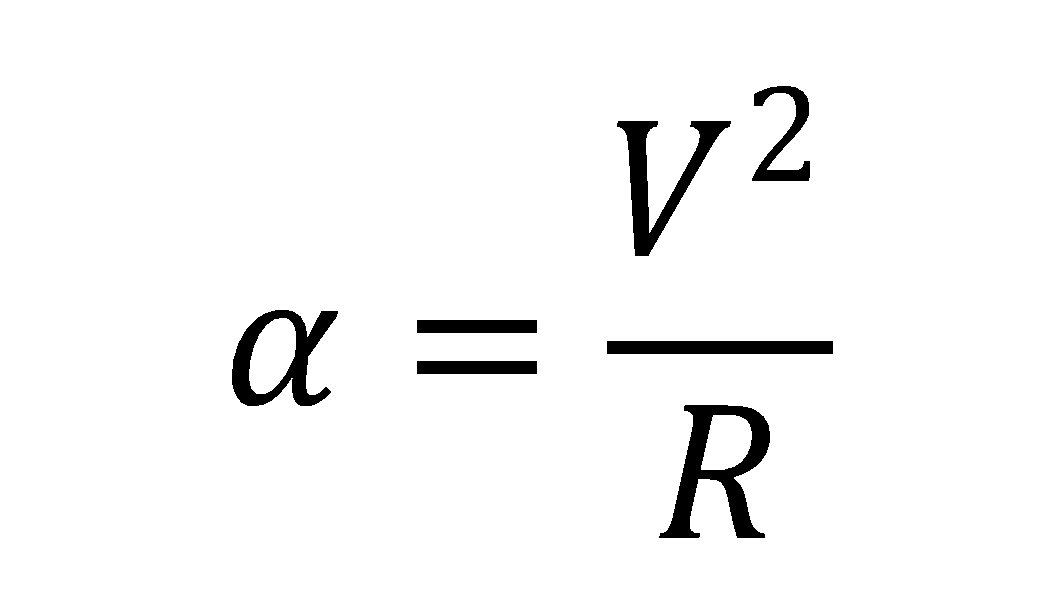
この3つの式を合わせると、
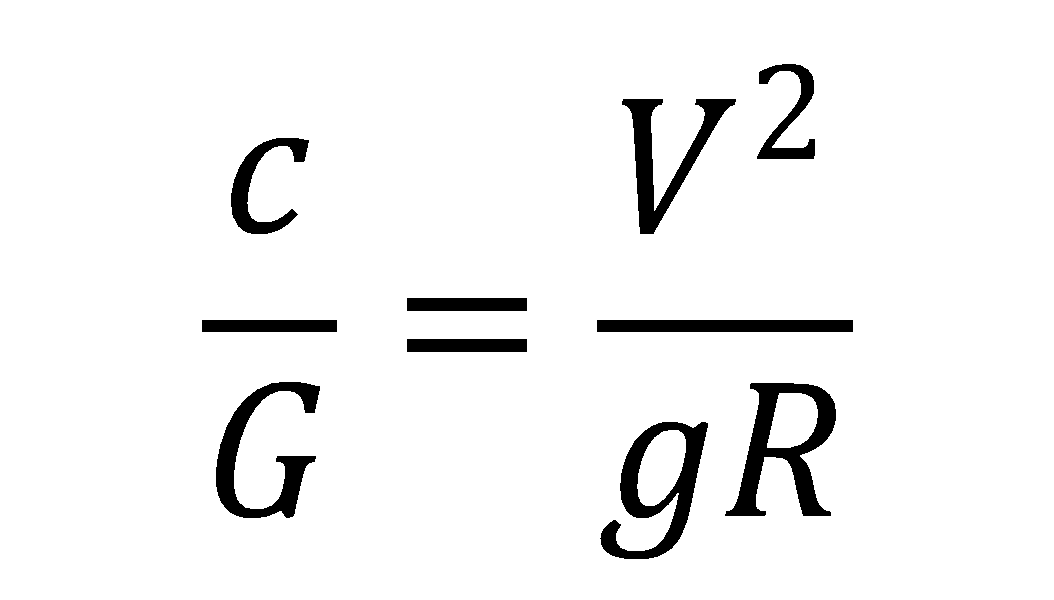
となり、この式を整えると、
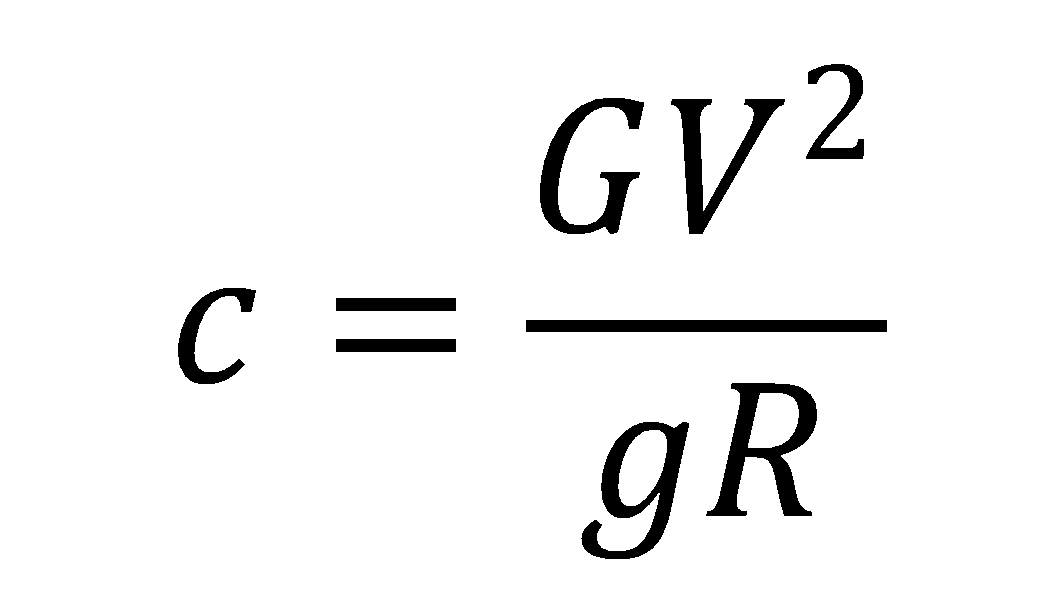
だいぶ件の公式に近づきます。
ここで忘れてはいけないのが、それぞれの単位です。一般的に速度Vは時速(km/h)で表すため、これを秒速(m/s)に直します。軌間Gはもともとミリメートルなのでそのまま(ものの長さはよくミリメートルで表現されます)。重力加速度g=9.8(m/s2)は秒速のため、このままです。そして求めたいカントcはミリメートルで計算したいため、1000分の1に直します。
換算すると、
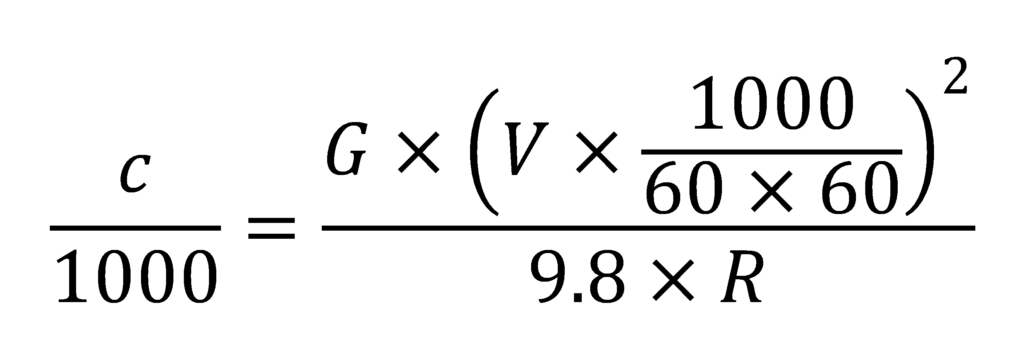
これを計算していくと、
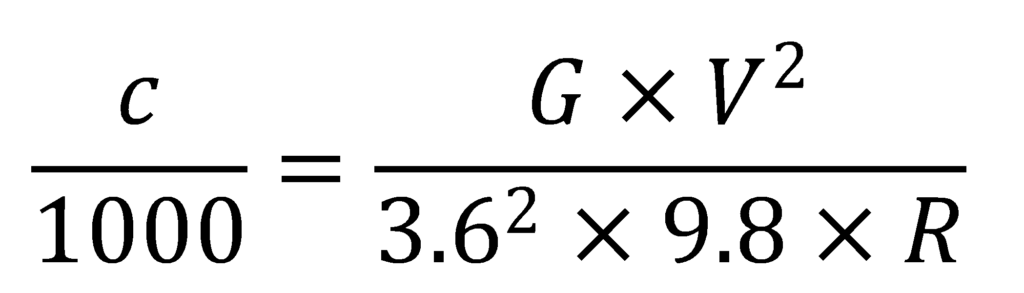
となって、
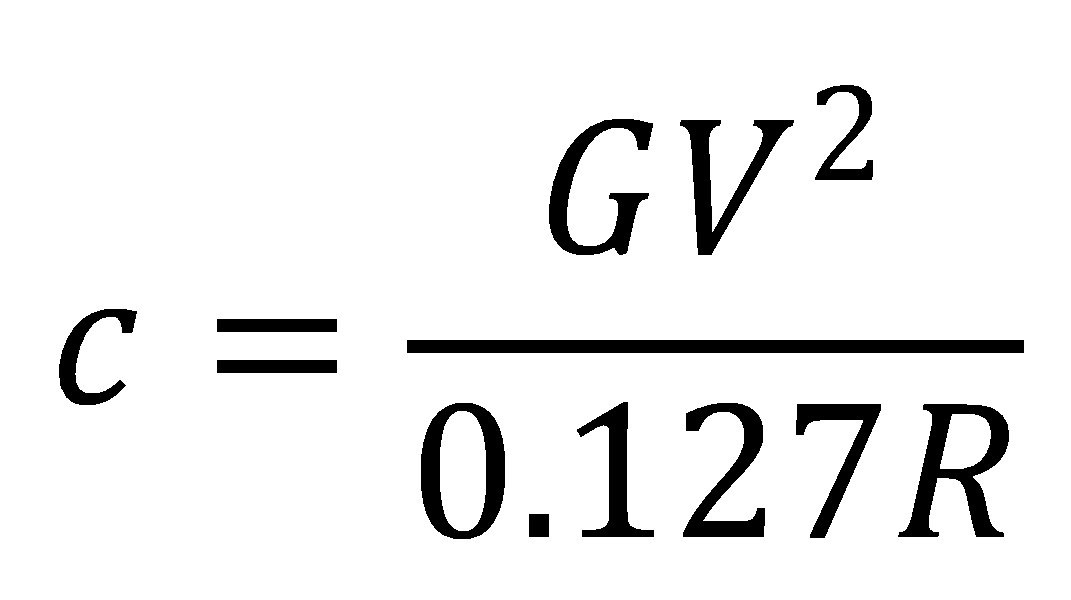
こうして、カントの式と、謎だった「0.127」が登場しました。単位換算によって出てきた数字だったのですね。
4.その後のこと
なお当時。この謎が解けた約1か月後に、質問をくださった方が「わかったよ!」とご自分でも解かれたことを伝えに再度来館してくださいました。「私もわかりました!」と一緒にお話させていただけたのは今でも嬉しい思い出ですし、学ぶ機会を頂けるのは本当にありがたい限りです。
質問の内容によっては館スタッフがすぐにお答えでき兼ねる内容・分野のものも多くあるため、できる限りお力になれるよう対応しています。その場でお答えできない場合もありますが、何卒ご容赦ください。
最後に、鉄道関係の研究者の方や詳しい方など、もしこのページを一読されて修正点やお気付きの点がございましたら、当館までご連絡いただけますと幸いです。
企画 K
<参考ウェブサイト>
“鉄道辞典_上巻 – 316/1046枚目”,公益財団法人 交通協力会ホームページ 鉄道資料 交通電子図書館,https://transport.or.jp/tetsudoujiten/HTML/1958_%E9%89%84%E9%81%93%E8%BE%9E%E5%85%B8_%E4%B8%8A%E5%B7%BB_P0287.html (参照:2024年12月)
